LINPACK Benchmark
Version 2.0
=================
Presented by University of Tennessee Knoxville and Innovative Computing Laboratory.
Implementation: Piotr Luszczek
This an optimized implementation of the LINPACK Benchmark. It is a yardstick of performance because it is widely used and performance numbers are available for almost all relevant systems.
The LINPACK Benchmark was introduced by Jack Dongarra. A detailed description as well as a list of performance results on a wide variety of machines is available in PostScript(TM) form from Netlib: http://www.netlib.org/benchmark/.
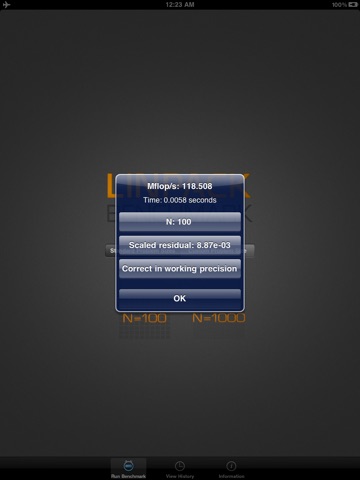
The test used in the LINPACK Benchmark is to solve a dense system of linear equations. The version of the benchmark for TOP500 allows the user to scale the size of the problem and to optimize the software in order to achieve the best performance for a given machine. This performance does not reflect the overall performance of a given system, as no single number ever can. It does, however, reflect the performance of a dedicated system for solving a dense system of linear equations. Since the problem is very regular, the performance achieved is quite high, and the performance numbers give a good correction of peak performance.
By measuring the actual performance for different problem sizes N, a user can get not only the maximal achieved performance Rmax for the problem size Nmax but also the problem size N_1/2 where half of the performance Rmax is achieved. These numbers together with the theoretical peak performance Rpeak are the numbers given in the TOP500. In an attempt to obtain uniformity across all computers in performance reporting, the algorithm used in solving the system of equations in the benchmark procedure must conform to the standard operation count for LU factorization with partial pivoting. In particular, the operation count for the algorithm must be 2/3 N*N*N + O(N*N) floating point operations. This excludes the use of a fast matrix multiply algorithms like "Strassians Method". This is done to provide a comparable set of performance numbers across all computers. If in the future a more realistic metric finds widespread usage, so that numbers for all systems in question are available, we may convert to that performance measure.